Deep Q-Learning Recap
In this article, basic concepts of Deep Q-Learning and Deep Q-Networks (DQNs) will be illustrated, and different techniques and improvements of DQNs will be discussed.
This article is based on Lecture 02/20/2017, CMU 10703 Deep Reinforcement Learning and Control, and some materials and paragraphs come from the lecture slides and the references listed at the end. The author, David Qiu (david@davidqiu.com), reserves all the rights of this article. Reposts of this article are allowed but they should clarify the authorship. If you have any question or correction suggestions, please feel free to contact the author.
若有疑惑,可以到知乎转载帖子里面留言,我的博客没有留言功能,实在抱歉:《知乎:Deep Q-Learning Recap》
Reinforcement Learning Components Review
An reinforcement learning agent may include one or more of the following components:
- Policy: A function representing the agent's behavior,
- Value Function: A function indicating how good each state and/or action is,
- Model: The agent's representation of the environment.
Reinforcement learning methods can be seperated into two types, model-based approaches and model-free approaches. Model-based approaches include a model that represents the state transition of the external environment, which is usually learnt from the past experiences of the agent, and exploits such a model to generate proper value function so as to discover an optimal policy. On the other hand, Model-free approaches does not include any model of the external environment, two primary methods of which are direct policy search and value function iteration. In direct policy search, the agent captures environment transitions at each running step and and takes advantage of such information to update its policy directly without storing any information about the dynamics of the environment. And in value function iteration, the agent takes advantage of the environmental transition information at each running step to update its value function and plans its policy in accord to its value function.
Policy
A policy represents an agent’s behavior at each state, which maps a state to an action.
A deterministic policy is one that maps each state to a specific action deterministically that
$$ \boldsymbol{a} \leftarrow \pi \left( \boldsymbol{s} \right) $$
where $( \boldsymbol{s} )$ is the state the agent is at, $( \pi )$ is the policy that the agent executes, and $( \boldsymbol{a} )$ is the action to take based on policy $( \pi )$.
A stochastic policy is one that considers the probability distribution of any action to take at a specific state. It suggests that in a specific state, the action that should be taken by the agent is not a specific one but various actions with their own probabilities of being taken at that state. Formally a stochastic policy can be expressed as
$$ P \left( \boldsymbol{a} \middle| \boldsymbol{s} \right) \leftarrow \pi \left( \boldsymbol{s}, \boldsymbol{a} \right) $$
where $( \boldsymbol{s} )$ is the state the agent is at, $( \boldsymbol{a} )$ is a possible action to take at state $( \boldsymbol{s} )$, $( \pi )$ is the policy that the agent executes, and $( P \left( \boldsymbol{a} \middle| \boldsymbol{s} \right) )$ is the probability that the agent takes action $( \boldsymbol{a} )$ at state $( \boldsymbol{s} )$ under policy $( \pi )$.
Value Function
A value function is a prediction of the long-term future rewards of a state or an action taken at a specific state. A state value function $( V )$ predicts how much reward the agent will get when reaching a state $( \boldsymbol{s} )$, while a state-action value function, or says a Q-value function, $( Q )$ predicts how much reward the agent will get by taking an action $( \boldsymbol{a} )$ at state $( \boldsymbol{s} )$.
Q-value Function
Q-value function gives expected total reward from state $( \boldsymbol{s} )$ and action $( \boldsymbol{a} )$ under policy $( \boldsymbol{\pi} )$ with discount factor $( \gamma )$ that
$$ Q^{\pi} \left( \boldsymbol{s}, \boldsymbol{a} \right) = \mathbb{E} \left[ r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + \cdots \middle| \boldsymbol{s}, \boldsymbol{a} \right] $$
Such a function could also decompose into a Bellman Equation form as
$$ Q^{\pi} \left( \boldsymbol{s}, \boldsymbol{a} \right) = \mathbb{E}_{ \boldsymbol{s}', \boldsymbol{a}' } \left[ r + \gamma Q^{\pi} \left( \boldsymbol{s'}, \boldsymbol{a'} \right) \middle| \boldsymbol{s}, \boldsymbol{a} \right] $$
Optimal Q-value Function
An optimal Q-value function is the maximum achievable value after taking an action $( \boldsymbol{a} )$ at a state $( \boldsymbol{s} )$, which is formally represented by
$$ Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) \leftarrow \max_{\pi} Q^{\pi} \left( \boldsymbol{s}, \boldsymbol{a} \right) \equiv Q^{ \pi^{*} } \left( \boldsymbol{s}, \boldsymbol{a} \right) $$
where $( \pi^{*} )$ is the optimal policy the agent could execute. Similarly, if we have the optimal Q-value function, it could yield the optimal policy at ease that
$$ \pi^{*} = \arg\max_{a} Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) $$
Moreover, an optimal Q-value function could formally decompose into the Bellman Equation form as
$$ Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) = \mathbb{E}_{ \boldsymbol{s'} } \left[ r + \gamma \max_{ \boldsymbol{a'} } Q^{*} \left( \boldsymbol{s'}, \boldsymbol{a'} \right) \middle| \boldsymbol{s}, \boldsymbol{a} \right] $$
Intuitively, an optimal Q-value function indicates the total expected sum of rewards gained at the future by taking the action sequence that yields the most rewards in total.
Deep Reinforcement Learning
As mentioned above, there are roughly three primary approaches to solving reinforcement learning problems, which are respectively
- Value-based approach, which estimates the optimal Q-value function $( Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) )$ that is the maximun sum of rewards achievable in future
- Policy-based approach, which searches directly for the optimal policy $( \pi^{*} )$ that is the policy achieving maximum future rewards
- Model-based approach, which builds a model of the environment and plan for a policy to execute using model (e.g. by look-ahead)
Deep reinforcement learning is acutally using deep neural networks to represent the components in classic reinforcement leanring problems. The components that could be represented by deep neural networks are
- Value function
- Policy
- Model
Due to the exhausting computational complexity, stochastic gradient descent (SGD) method is usually employed in the loss function optimization for these neural networks.
Deep Q-Networks
An advantage of using neural networks in representing a Q-value function is that it they could handle the continuity of the state space and the action space. In cases where the state space and action space are both continuous, the Q-Network structure with both state and action as input and an output number that indicates the value of taking such an action in such a state is usually employed. But in some cases, where action space is discrete, there would be some tricks to save computational resources.
The following are two structures of Deep Q-Networks design.
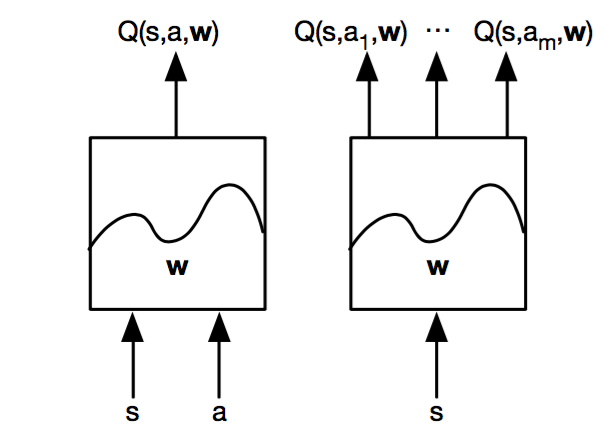
The left DQN structure is generally applicable to both discrete and continuous action space, and the structure, proposed by Google DeepMind (reference requested), to the right is applicable to discrete action space. A Significant advantage of the structure to the right is that it can generate all the action values for a specific state at once and save a lot of computational resources.
Our goal of learning here is to learn the parameter vector $( \boldsymbol{w} )$ which contains all the weights of a Q-Network that approximates the true optimal value function $( Q^{*} )$ that
$$ Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \approx Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) $$
for each state $( \boldsymbol{s} )$ in the state space and each action $( \boldsymbol{a} )$ in the action space.
However, it is impossible to obtain the actual optimal Q-value function $( Q^{*} )$, otherwise we do not have to train a Q-Network that approximates the true optimal Q-value function and we should just use the true optimal Q-value function instead. Formally the true optimal Q-value function is
$$ Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) = \mathbb{E}_{ \boldsymbol{s'} } \left[ r + \gamma \max_{ \boldsymbol{a'} } Q^{*} \left( \boldsymbol{s'}, \boldsymbol{a'} \right) \middle| \boldsymbol{s}, \boldsymbol{a} \right] $$
where the right-hand term in this equation is the learning target given state $( \boldsymbol{s} )$ and action $( \boldsymbol{a} )$. But we could not obtain the real value of the expectation term. Instead, what we could do is to assume that the Q-Network we have trained so far is a (good) approximation to the true Q-value function, so we could approximate the right-hand term with our current Q-Network, which is formally
$$ r + \gamma \max_{a'} Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w} \right) \approx \mathbb{E}_{ \boldsymbol{s'} } \left[ r + \gamma \max_{ \boldsymbol{a'} } Q^{*} \left( \boldsymbol{s'}, \boldsymbol{a'} \right) \middle| \boldsymbol{s}, \boldsymbol{a} \right] \equiv Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) $$
Some people may be confused here, because it seems we are training the Q-Network with information generated by itself. It is true that part of the target information is from the Q-Network itself, but do not forget there is a ground-truth reward term $( r )$ to fix the error. It works very similarly to TD-Learning, where bootstrapping is used to gradually update the Q-value function approximation. Here we use the bootstrapping technique along with the future rewards approximated by the Q-Network itself and the ground-truth reward term to update the Q-Network parameters towards the true Q-value function gradually.
And our goal of learning is now a goal of optimization on minimizing the mean-squared error (MSE) loss
$$ \begin{align*} l & = \left( Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right)^{2} \\ & \approx \left( r + \gamma \max_{a} Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right)^{2} \end{align*} $$
And then we apply stochastic gradient descent (SGD) to optimize the above MSE loss so as to make the Q-Network more close the the true optimal Q-value function. We use stochastic gradient descent instead of gradient descent here because of the computational complexity. And SGD could optimize the weights of the Q-Network to be close enough to those optimized with gradient descent method if we have trained for enough number of epochs.
If we are using table lookup representation of the MSE, the lookup table will converge to the true Q-value function $( Q^{*} )$. But in continuous cases, the Q-Network may diverge due to:
- Correlations between samples (i.e. the state-action pairs show up in a specifc order in the training set)
- Non-stationary targets (i.e. the Q-Network changes after each training epoch which leads to non-stationary targets for the learning process)
In the following section, we are going to discuss how to overcome these undesirable effects.
Experience Replay
A trick called the experience replay is designed to handle the correlations between samples. If there are strong correlations between samples, the Q-Network may bias to a specific direction when training with a set of samples, and it may bias to another direction when training with another set of samples. To handle this problem, we need to break the correlations of the samples, so as to training the Q-Network towards an average direction. With this demand, the technique named experience replay is proposed.
In experience replay, past state-action pairs are stored in a memory with limited or unlimited length, which means the memory may store a specific amount of latest state-action pairs or just store all of them from the past experience. After then, in each learning epoch, a set of a small number of state-action pairs are randomly chosen from the memory to form a training set to train the Q-Network, where such a set of training samples is called a mini-batch. This technique could break the correlations because it is randomly choosing different state-action pair from the memory, rather than choosing them in order. So the observation order of the state-action pair does not matter in the training process, thus the correlations are removed.
Formally, during the experience remembering process, the new experience as a state-action pair is stored to the memory that
$$ D_{t+1} \leftarrow D_{t} \cup \left\{ \left\langle \boldsymbol{s}_{t}, \boldsymbol{a}_{t}, r_{t+1}, \boldsymbol{s}_{t+1} \right\rangle \right\} $$
During the training process, multiple state-action pairs are randomly chosen from the memory to form a mini-batch for training the Q-Network that
$$ \left\langle \boldsymbol{s}, \boldsymbol{a}, r, \boldsymbol{s'} \right\rangle \sim \text{Uniform} \left( D \right) $$
And then apply stochastic gradient descent to update the weight vector of the Q-Network by adding to the weight vector a difference
$$ \triangle \boldsymbol{w} = - \alpha \frac{ \partial l }{ \partial \boldsymbol{w} } $$
where $( \alpha )$ is the learning rate, $( l )$ is the mean-squared loss function of the weight $( \boldsymbol{w} )$ and $( \triangle \boldsymbol{w} )$ is weight vector difference to add to the current weight vector so as to update the Q-Network. The partial derivative of the loss function with respect to the weight vector is
$$ \begin{align*} \frac{ \partial l }{ \partial \boldsymbol{w} } & = \frac{ \partial }{ \partial \boldsymbol{w} } \left( Q^{*} \left( \boldsymbol{s}, \boldsymbol{a} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right)^{2} \\ & \approx \frac{ \partial }{ \partial \boldsymbol{w} } \left( r + \gamma \max_{a} Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w}^{-} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right)^{2} \\ & = - 2 \left( r + \gamma \max_{a} Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w}^{-} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right) \triangledown_{ \boldsymbol{w} } Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \end{align*} $$
where the coefficient $( 2 )$ can be considered as part of the learning rate $( \alpha )$, so the weight vector difference can be formally expressed as
$$ \triangle \boldsymbol{w} = \alpha \left( r + \gamma \max_{a} Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w}^{-} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right) \triangledown_{ \boldsymbol{w} } Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) $$
where $( \boldsymbol{w}^{-} \equiv \boldsymbol{w} )$ in the above two equations, which is equal to the value of the weight vector but considered as a constant in derivative.
Fixed Parameters
To deal with non-stationarity, the weight vector $( \boldsymbol{w}^{-} )$ in the learning target term is held fixed. If this parameter is fixed instead of changing after each traning epoch, the non-stationary targets issue is solved, because the training target is now fixed, or says stationary.
Practically, however, the target weight vector term could not be held fixed all the time, otherwise the Q-Network could never get close to the true Q-value function. In order to train the Q-Network practically, we need to update the target weight vector term after certain epochs of training.
So intuitively, there are actually two Q-Networks, which are respectively the training network with parameter $( \boldsymbol{w} )$ and the target network with parameter $( \boldsymbol{w}^{-} )$. The training network will be updated at each training epoch, and after certain training epochs, the parameter of the training network is assigned to that of the target network to update the target network that
$$ \boldsymbol{w}^{-} \leftarrow \boldsymbol{w} $$
The training target is now stationary within certain training epochs, after that the training target is updated with the new weight vector, and this process repeats at each training phase.
Double Q-Learning
Double Q-Learning was proposed in the Double Q-learning, Hado van Hasselt, 2010, which served as an alternative to handle the non-stationarity issue. A single Q-value function approximation may engender non-stationarity because the Q-value function approxiamtion is intuitively like trying to approximate itself by itself, so the targets always change after each training epoch. Double Q-Learning tries to handle this problem by introducing a second Q-value function approximation, so that a Q-value function approximation is always trained by using the information from the other Q-value function approximation. And from the prospective of either approximation, the training target is relatively stationary, because they are not training itself with the information from itself.
Formally, we have two Q-value function approximations in double Q-Learning problem, denoted by $( Q_{1} )$ and $( Q_{2} )$. During the action selection process, the action that renders the maximun sum of the two Q-value functions is picked and $( \epsilon )$-greedy policy with this selected action is executed. In other words, the action selected to execute $( \epsilon )$-greedy policy at a specific state $( \boldsymbol{s} )$ is formally
$$ \boldsymbol{a} \leftarrow \arg\max_{ \boldsymbol{a} } \left[ Q_{1} \left( \boldsymbol{s}, \boldsymbol{a} \right) + Q_{2} \left( \boldsymbol{s}, \boldsymbol{a} \right) \right] $$
After an action generated by the $( \epsilon )$-greedy policy is actually executed, a reward $( r )$ and a following state $( \boldsymbol{s'} )$ are observed. In the update process, either of the following equations is chosen to execute with each having a probability to be chosen by $( 0.5 )$. The equation to execute so as to update only one of the Q-value function approximations at a timestep in an episode is either
$$ Q_{1} \left( \boldsymbol{s}, \boldsymbol{a} \right) \leftarrow Q_{1} \left( \boldsymbol{s}, \boldsymbol{a} \right) + \alpha \left[ r + \gamma Q_{2} \left( \boldsymbol{s'}, \arg\max_{ \boldsymbol{a'} } Q_{1} \left( \boldsymbol{s'}, \boldsymbol{a'} \right) \right) - Q_{1} \left( \boldsymbol{s}, \boldsymbol{a} \right) \right] $$
or
$$ Q_{2} \left( \boldsymbol{s}, \boldsymbol{a} \right) \leftarrow Q_{2} \left( \boldsymbol{s}, \boldsymbol{a} \right) + \alpha \left[ r + \gamma Q_{1} \left( \boldsymbol{s'}, \arg\max_{ \boldsymbol{a'} } Q_{2} \left( \boldsymbol{s'}, \boldsymbol{a'} \right) \right) - Q_{2} \left( \boldsymbol{s}, \boldsymbol{a} \right) \right] $$
So during updating one Q-value function approximation, the other is held fixed to assure target stationarity. An obvious significance of this method compared to the fixed parameters method is that there is no hyperparameter of how long the target function parameters should be held fixed, and instead, the two Q-value function approximations alternate to provide stationarity.
Double DQNs
Similarly, double Q-leanring could be extended into Double Deep Q-Networks (Double DQNs) by approximating the true Q-value function with two neural networks, or says two weight vectors $( \boldsymbol{w}_{1} )$ and $( \boldsymbol{w}_{2} )$ applied to the same Q-Network structure. This work is proposed in Deep Reinforcement Learning with Double Q-learning, Hado van Hasselt, Arthur Guez, David Silver, 2015.
During the action selection process, the action that renders the maximun sum of the two Q-Networks is picked and $( \epsilon )$-greedy policy with this selected action is executed. The action selected to execute the $( \epsilon )$-greedy policy at a specific state $( \boldsymbol{s} )$ is formally
$$ \boldsymbol{a} \leftarrow \arg\max_{ \boldsymbol{a} } \left[ Q_{1} \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w}_{1} \right) + Q_{2} \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w}_{2} \right) \right] $$
And during the update process, one weight vector is chosen as the training network weight vector $( \boldsymbol{w} )$ and the other is chosen as the target network weight $( \boldsymbol{w}_{-} )$. In other words, either
$$ \boldsymbol{w} \leftarrow \boldsymbol{w}_{1}, \boldsymbol{w}^{-} \leftarrow \boldsymbol{w}_{2} $$
or
$$ \boldsymbol{w} \leftarrow \boldsymbol{w}_{2}, \boldsymbol{w}^{-} \leftarrow \boldsymbol{w}_{1} $$
is chosen with each have a probability by $( 0.5 )$ at each timestep in an episode. And the following MSE loss function is optimized to train the training Q-Network weight vector $( \boldsymbol{w} )$ that
$$ l = \left( r + \gamma Q \left( \boldsymbol{s'}, \arg\max_{ \boldsymbol{a'} } Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w} \right), \boldsymbol{w}^{-} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right)^{2} $$
With the same conclusion derived in the previous section, update difference of the traning weight vector is then
$$ \triangle \boldsymbol{w} = \alpha \left( r + \gamma \max_{a} Q \left( \boldsymbol{s'}, \arg\max_{ \boldsymbol{a'} } Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w} \right), \boldsymbol{w}^{-} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right) \triangledown_{ \boldsymbol{w} } Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) $$
Repeat the above action selection and update process in each timestep, and the two Q-Networks are expected to converge to the true Q-value function online.
Prioritized Replay
The prioritized replay technique is proposed in Prioritized Experience Replay, Tom Schaul, John Quan, Ioannis Antonoglou, David Silver, 2016. Its primary concept is to choose training samples from the memory to train the Q-Network considering the priorities of different samples in the memory. The samples that generate larger mean-squared errors have higher priorities to be chosen to form the mini-batch during a training epoch. Intuitively, it is trying to optimize the MSE loss function by samples that renders larger errors, so that after a certain traning epochs, the errors for different samples would get closer to each other, which means such an optimization process tend to lead the Q-Network towards the average direction of all samples.
Practically, we consider the absolute value of the error
$$ p_{i} = \left| r + \gamma \max_{a'} Q \left( \boldsymbol{s'}, \boldsymbol{a'}, \boldsymbol{w}^{-} \right) - Q \left( \boldsymbol{s}, \boldsymbol{a}, \boldsymbol{w} \right) \right| $$
where $( i )$ is the index of the samples in the memory, and each sample is a tuple $( \left\langle \boldsymbol{s}, \boldsymbol{a}, r, \boldsymbol{s'} \right\rangle )$ with $( \boldsymbol{s} )$ being the previous state, $( \boldsymbol{a} )$ the action taken, $( r )$ the reward gained and $( \boldsymbol{s'} )$ the following state.
In deterministic cases, samples are chosen to form a mini-batch considering the samples with the largest absolute errors.
While in stochastic prioritization, the probability of each sample being chosen to form a mini-batch is defined as
$$ P \left( i \right) = \frac{ p_{i}^{\alpha} }{ \sum_{k} p_{k}^{\alpha} } $$
where the parameter $( \alpha )$ here determines how much prioritization is used with $( \alpha = 0 )$ corresponding to the uniform distribution for choosing samples from the memory.
Dueling Networks
The concept of dueling networks is proposed in Dueling Network Architectures for Deep Reinforcement Learning, Ziyu Wang et.al., 2016. The idea of dueling networks is to seperate the effects brought by the state the agent is at and the action the agent takes into two channels, the action-independent value function $( V \left( \boldsymbol{s} \right) )$ and action-dependent advantage function $( A \left( \boldsymbol{s}, \boldsymbol{a} \right) )$. Formally the relationship of these two functions could be represented by the following equation that
$$ Q \left( \boldsymbol{s}, \boldsymbol{a} \right) = V \left( \boldsymbol{s} \right) + A \left( \boldsymbol{s}, \boldsymbol{a} \right) $$
where $( Q )$ is the Q-value function, or says the state-action function. With the equation stated above, we could defined the advantage function as
$$ A^{\pi} \left( \boldsymbol{s}, \boldsymbol{a} \right) = Q^{\pi} \left( \boldsymbol{s}, \boldsymbol{a} \right) - V^{\pi} \left( \boldsymbol{s} \right) $$
where $( \pi )$ is the policy that the agent executes, $( \boldsymbol{s} )$ is the state that the agent is at, $( \boldsymbol{a} )$ is the action taken by the agent at state $( \boldsymbol{s} )$, $( Q^{\pi} )$ is the Q-value function considering state and action under policy $( \pi )$, $( V^{\pi} )$ is the state value function considering only the state under policy $( \pi )$ and $( A^{\pi} )$ the advantage function considering the state and action under policy $( \pi )$ but it mainly reflects the advantage of taking an action under a specific state and removes the advantage of being at this state.
Intuitively, it is like considering the value of being at a state and the value of taking an action in a specific state. If we use the Q-value function, the measurement of the action taken at a specific state has a bias rendered by being at that state. In other words, the Q-value being good does not mean the action is very good, but it happens maybe just because the agent is at a very good state; on the other hand, a bad Q-value does not render a bad choice of action, which happens maybe just because of being at a very bad state. So the advantage function is actually a measurement of how good the choice of an action is without the bias of the how good a state the agent is at.
In the original paper, neural networks are employed to approximate the value function $( V )$ and advantage function $( A )$. A comparision between the popular Q-Network design and the dueling networks are shown below.
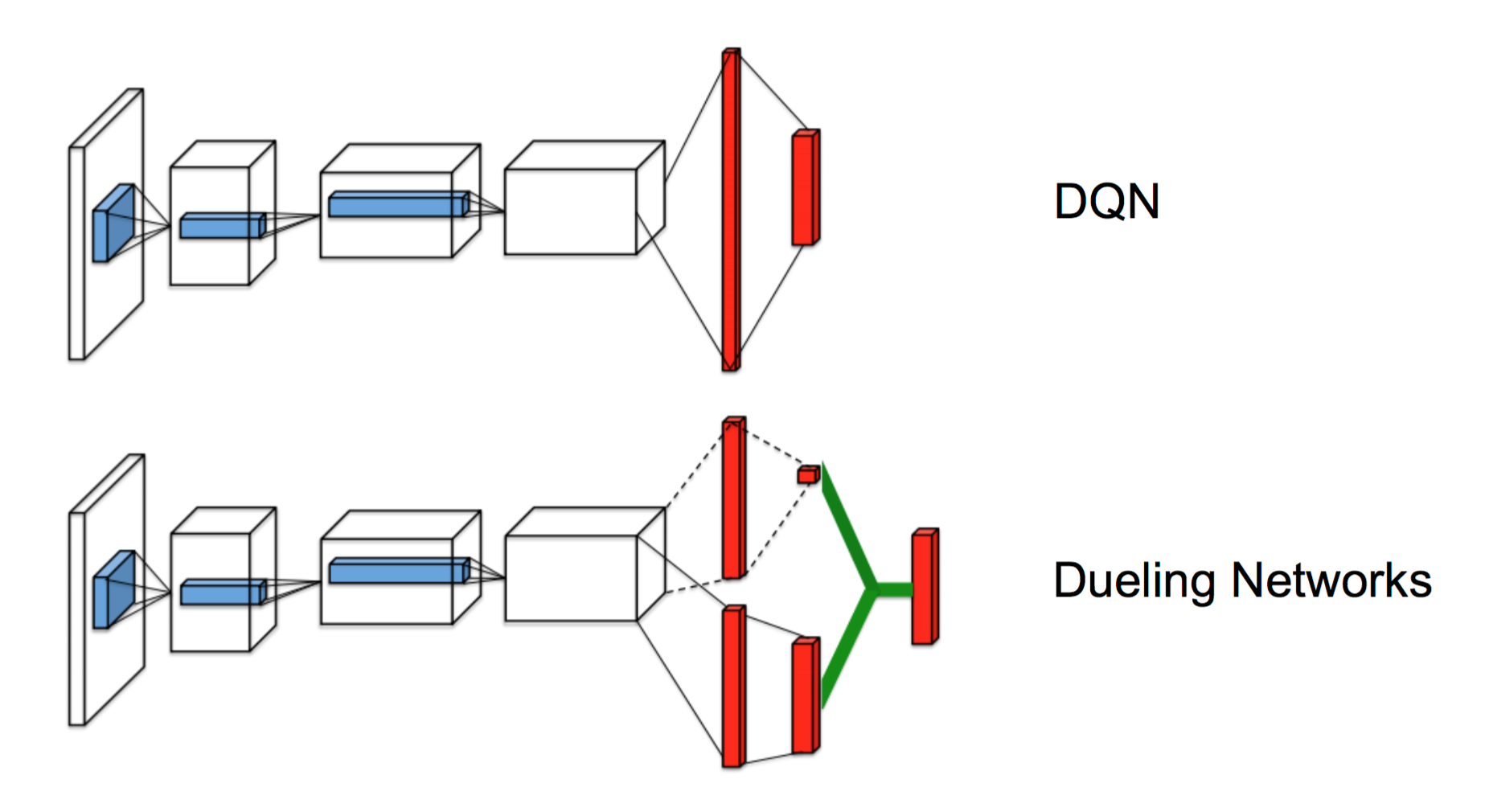
More precisely, the dueling architecture consists of two streams that represent the value and advantage functions, while sharing a common convolutional feature learning module. The two streams are combined via a special aggregating layer to produce an estimate of the state-action value function $( Q )$. This dueling network should be understood as a single Q network with two streams that replaces the popular single-stream Q network in existing algorithms such as Deep Q-Networks (DQNs). The dueling network automatically produces separate estimates of the state value function and advantage function, without any extra supervision.
Mulitask DQNs and Transfer Learning
Related works about multitask DQNs and transfer learning with a method called Actor-Mimic are proposed in Actor-Mimic: Deep Multitask and Transfer Reinforcement Learning.
The idea of multitask DQNs is that a single Q-Network can learning to play across different games. Although the original DQN maintains the same network architecture and hyperparameters for all games, the approach is limited in the fact that each network only learns how to play a single game at a time, despite the existence of similarities between game. A network trained to play multiple games would be able to generalize its knowledge between the games, achieving a single compact state representation as the inter-task similarities are exploited by the network.
Having been trained on enough source tasks, the multitask network can also exhibit transfer to new target tasks, which can speed up learning. Training deep reinforcement learning agents can be extremely computationally intensive and therefore reducing training time is a significant practical benefit. And this is the idea of transfer learning.
References
- Lecture 02/20/2017, CMU 10703 Deep Reinforcement Learning and Control
- Double Q-learning, Hado van Hasselt, 2010
- Deep Reinforcement Learning with Double Q-learning, Hado van Hasselt, Arthur Guez, David Silver, 2015
- Prioritized Experience Replay, Tom Schaul, John Quan, Ioannis Antonoglou, David Silver, 2016
- Dueling Network Architectures for Deep Reinforcement Learning, Ziyu Wang et.al., 2016
- Actor-Mimic: Deep Multitask and Transfer Reinforcement Learning